Big Ω 란
Definition: (Asymptotic Lower Bound)

N보다 큰 모든 부분에서 f(n) 에 어떤 양의 실수 c를 곱한 값이 g(n) 보다 작은 값으로 존재하는 것.
N보다 작은 부분은 상관없다. g(n) ∈ Ω(f(n)
g(n) ≥ c × f(n)
g(n) ∈ Ω(f(n) 의 의미
N보다 작은 부분에서는 cf(n)이 g(n)보다 크지만, 결국에는 N 보다 큰 모든 부분에서 cf(n) 보다 커져서 cf(n) 위에 머무르게 된다.
g(n)이 알고리즘의 시간 복잡도라면 결국 알고리즘의 실행 시간은 최소한 f(n) 보다는 크거나 같도록 갖게 된다.
g(n)은 f(n)보다 빠르게 실행될 수 없다.
n^2+10n∈Ο(n^2) ?
c =1 , N=0 이면 모든 실수 n≥ 0에 대하여 n^2+10n≥n^2 이 성립한다.
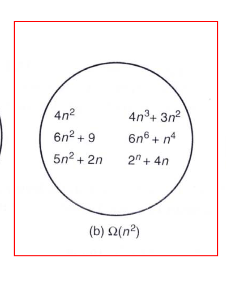
따라서 n^2 은 n^2+10n 에 Big Ω (asymptotic lower bound)를 만족한다. (I.e., n2+10은 Ω(n^2) 에 속한다,)
5n^2 ∈Ω(n2)
c =1 , N=0 이면 모든 실수 n≥ 0에 대하여 , 5n^2≥ n^2 이 성립한다.
따라서 n^2 은 5n^2에 Big Ω (asymptotic lower bound)를 만족한다. (I.e., 5n^2은 Ω(n^2) 에 속한다.)
n^3∈ Ω (n^2)?
양변을 n^2으로 나누면 1>= c n 식을 얻게 된다. 1/n >=c 는 변수 n이 충분히 커진다면 0에 가까워 지므로 0에 한없이 가까운 양의 상수 c가 존재하는 것은 불가능하므로 n^3∈ Ω (n^2) 속하지 않는다.
Big-Θ 란
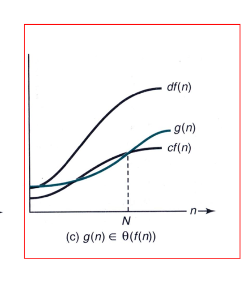
Definition: (Asymptotic Tight Bound)
N보다 큰 모든 부분에서 f(n) 에 어떤 양의 실수 c, d 가 있을 때 c * f(n)< = g(n) <= d*f(n) 사이의 값으로 존재하는 것

Small o 란
N보다 큰 모든 부분에서 f(n) 에 모든 양의 실수 c를 곱한 값이 g(n) 보다 큰 값으로 존재하는 것.
N보다 작은 부분은 상관없다. g(n) ∈ o(f(n))
g(n) <= c* f(n)
Big O vs. Small o 차이는 어떤 양의 실수 c와 모든 양의 실수 c 차이 뿐이다.
n∈o(n^2)?
c > 0 일때 n < cn^2 이고 양변을 cn으로 나누면 1/c < n 이다.
예를 들어 c=0.00001일 때 N은 100,000 이다.
n∈o(5n) ?
c = 1/6라 가정하면 If n∈o(5n), n <= 5/6 n 을 만족하지 못하므로 o(5n)에 속하지 않는다.
small o 관계를 만족시키려면 g(n)이 f(n) 보다 효율적인 알고리즘이여야 한다.
ex) g(n)=n , f(n) =n^2 일 떄 가능 , g(n)=n, f(n)=5n 일 때 불가능
Using a Limit to Determine Order

확실히 값을 특정하지 못하면, 로피탈의 정리를 사용하여 값을 구하여, order를 특정한다.

'스터디 > 알고리즘 설계와 분석' 카테고리의 다른 글
| 알고리즘 (Big O Notation) (1) | 2023.10.27 |
|---|---|
| 알고리즘 분석 (0) | 2023.10.27 |
| 알고리즘 (피보나치 재귀,DP 비교) (1) | 2023.10.26 |
| 알고리즘 - 탐색 (순차 탐색, 이분 탐색 ) (0) | 2023.10.26 |
| 알고리즘 설계 (0) | 2023.10.26 |
