Representatvie Order Fuctions
Θ(lg n) (로그 시간 복잡도):
이 함수는 로그 시간 복잡도를 나타내고 주로 이진 검색과 같이 큰 데이터 집합에서 효율적인 검색 알고리즘에 적용된다 . 시간이 데이터의 크기에 대해 로그 성장한다.
Θ(n) (선형 시간 복잡도):
이 함수는 선형 시간 복잡도를 나타내고 시간이 입력 크기에 비례하여 선형적으로 증가한다. 예를 들어, 리스트의 모든 요소를 한 번 씩 훑는 경우에 해당한다.
Θ(n lg n) (선형로그 시간 복잡도):
이 함수는 선형로그 시간 복잡도를 나타낸다. 주로 효율적인 정렬 알고리즘인 병합 정렬(Merge Sort)과 퀵 정렬(Quick Sort)과 관련이 있다.
Θ(n^2) (제곱 시간 복잡도):
이 함수는 제곱 시간 복잡도를 나타낸다. 이는 주로 버블 정렬(Bubble Sort)이나 삽입 정렬(Insertion Sort)과 같은 비효율적인 정렬 알고리즘에 해당한다. 시간이 입력 크기의 제곱에 비례하여 증가한다.
Θ(n^3) (세제곱 시간 복잡도):
이 함수는 세제곱 시간 복잡도를 나타낸다. 이는 주로 세제곱 시간 복잡도를 갖는 알고리즘에 해당한다,
Θ(2^n) (지수 시간 복잡도):
이 함수는 지수 시간 복잡도를 나타낸다. 이는 주로 재귀적인 방식으로 문제를 해결하는 경우에 해당하며, 입력 크기가 커질수록 시간이 급격하게 증가합니다.
Θ(n!) (계승 시간 복잡도):
이 함수는 계승 시간 복잡도를 나타낸다. 이는 대규모 계산 및 순열과 조합과 같이 매우 복잡한 조합론적 문제에 해당하며, 입력 크기가 커질수록 시간이 급격하게 증가한다.
Growth Rates of Some Complexity Functions
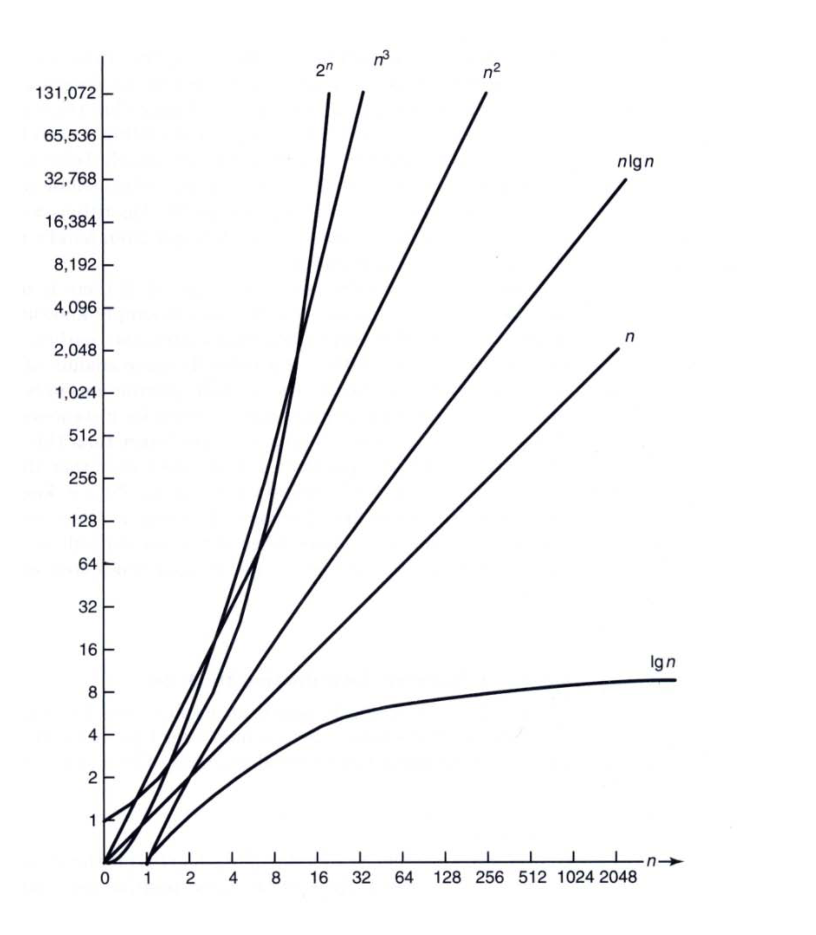
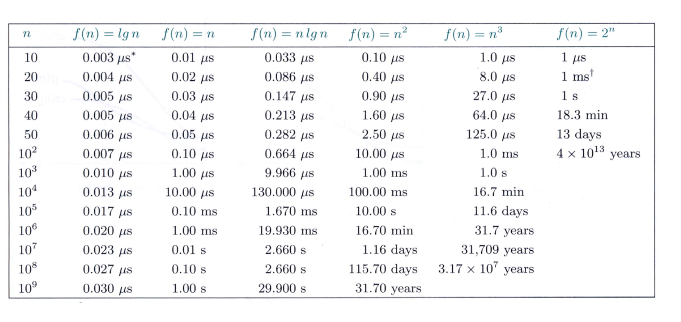
서로 다른 시간 복잡도를 갖는 각 함수의 실행 시간
Big O 란
Definition: (Asymptotic Upper Bound)

N보다 큰 모든 부분에서 f(n) 에 어떤 양의 실수 c를 곱한 값이 g(n) 보다 큰 값으로 존재하는 것.
N보다 작은 부분은 상관없다. g(n) ∈Ο(f(n))

g(n) ≤ c × f(n)
g(n) ∈Ο(f(n))의 의미
N보다 작은 부분에서는 g(n)이 cf(n) 보다 크지만,결국에는 N 보다 큰 모든 부분에서 cf(n) 아래로 떨어져 f(n) 아래에 머무르게 된다.
g(n)이 알고리즘의 시간 복잡도라면 결국 알고리즘의 실행 시간은 f(n) 보다는 작거나 같도록 갖게 된다.
f(n)이 점근적 상환이 된다. 즉, g(n)은 f(n)보다 느리게 실행될 수 없다.
예시)
n^2+10n∈Ο(n^2) ?
Take c = 2 and N = 10
n^2+10n < = 2n^2 10보다 큰 모든 실수에서 성립한다.

n∈Ο(n^2) ?
c = 1 and N = 1라 하면 1보다 모든 큰 실수에서 n≤ 1×n^2 가 성립한다.
n^3∈Ο(n^2)?
양변을 n^2으로 나누면 n≤c 식을 얻게 된다.그러나 변수 n보다 충분히 큰 상수 c가 존재하는 것은 불가능하므로
n^3 ∈ Ο(n^2) 에 속하지 않는다.
'스터디 > 알고리즘 설계와 분석' 카테고리의 다른 글
| 알고리즘 (Big-Ω, Big-Θ, small-o) (0) | 2023.10.27 |
|---|---|
| 알고리즘 분석 (0) | 2023.10.27 |
| 알고리즘 (피보나치 재귀,DP 비교) (1) | 2023.10.26 |
| 알고리즘 - 탐색 (순차 탐색, 이분 탐색 ) (0) | 2023.10.26 |
| 알고리즘 설계 (0) | 2023.10.26 |
